报名编号:CICC4035
团队名称:守序善良队
大家好,本篇是我们队伍的第二篇分享,主要内容是介绍Verilog实现使用Booth编码和Wallace树的定点补码乘法器原理。水平有限,如有错误,欢迎大家批评指正。
对于有符号整数乘法操作,E203使用常用的Booth编码产生部分积,然后使用迭代的方法,每个周期使用加法器对部分积进行累加,经过多个周期的迭代之后得到最终的乘积。其基本硬件原理图如图所示,从而实现多周期乘法器。乘法器,对于无符号乘法进行一位符号扩展后统一当作有符号数进行运算,因此需要17个迭代周期。为了改良乘法器性能,我们可以使用Booth编码和Wallace树的定点补码乘法器,该乘法器生成运算结果只需要一个周期,大大提升了乘法器性能。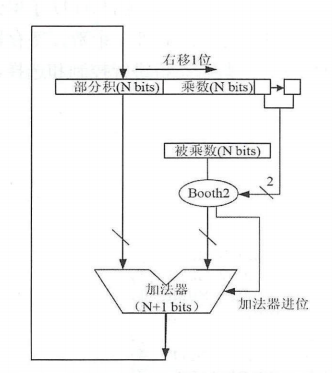
将乘数看作从最低位开始的一串二进制数字。Booth算法的基本思路是:对于具有连续0和1的组,需要产生的部分积较少。对于乘数中每个0,仅需要将前面的累加的部分积向右移动一位。
Booth编码采用相加和相减的操作计算补码数据的乘积,可以减少部分积的数目,用来计算有符号乘法,提高乘法运算的速度。
Booth算法一次看乘数的两个位依照目前与先前位的不同,执行下面工作:
00:字符串0的中间部份,不需要算术运算
01:字符串1的结尾,所以将乘数加到乘积的左半部
10:字符串1的开端,所以从乘积的左半部减去乘数
11:字符串1的中间部份,不需要算术运算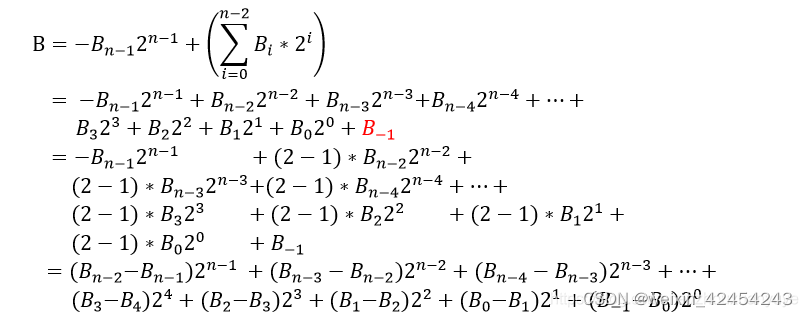
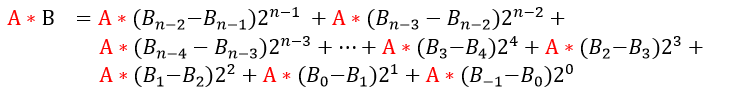
在一个乘法阵列中,把同一列中的部分积(位)与右边一列传来的进位通过CSA或其它位数压缩电路(尽可能早地)相加,所产生的Carry-out送向左边一列,所产生的“和”位继续在本列传播,这就构成了Wallace Tree乘法器。
Wallace树充分利用全加器3-2压缩的特性,随时将可利用的所有输入和中间结果及时并行计算,大大节省了计算延时。下图是Wallace树型结构和CSA结构的对比。其结构的关键特性在于利用不规则的树形结构对所有的准备好输入数据的运算及时并行处理。
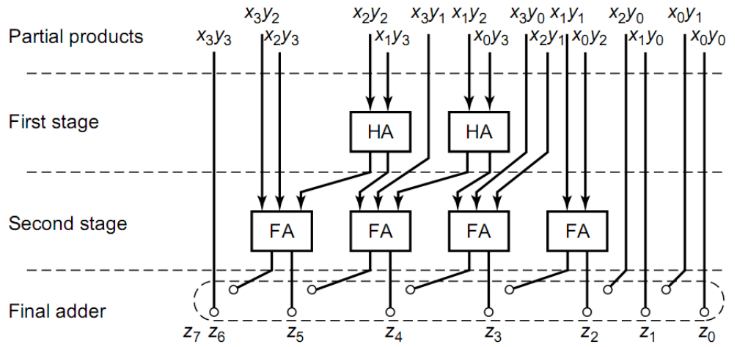
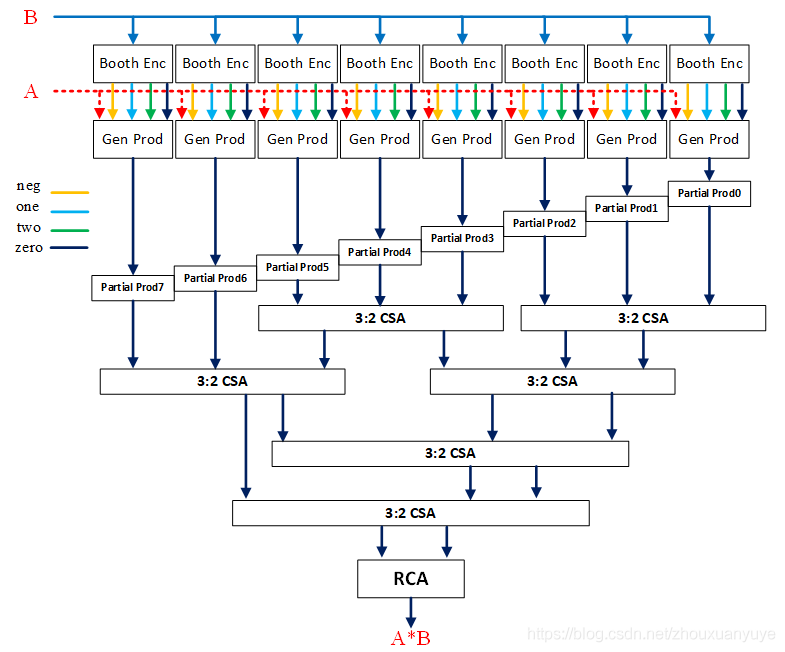
在华莱士树中,对于16位乘法,其每位至少包含6个全加器。对于32位乘法,全加器个数则为14。这样子做可以保证对于首位,其有6/14个空闲的进位要求,这至少可满足n-2个末尾加法操作,剩下的两个一个用在C和S的加法器进位输入,一个用在C左移一位的0号位置上,就满足了减去操作的补码部分积处理。
参考文章:
《手把手教你设计CPU》