团队:站着撸代码
双线性插值法:目标象素值根据这个源图中虚拟的点四周的四个真实的点来按照一定的规律计算出来。像最邻近插值法那样由目标图的坐标反推得到的源图的的坐标是一个浮点数的时候,采用了四舍五入的方法,直接采用了和这个浮点数最接近的象素的值,这种方法是很不科学的,双线性插值法算是它的改进吧。
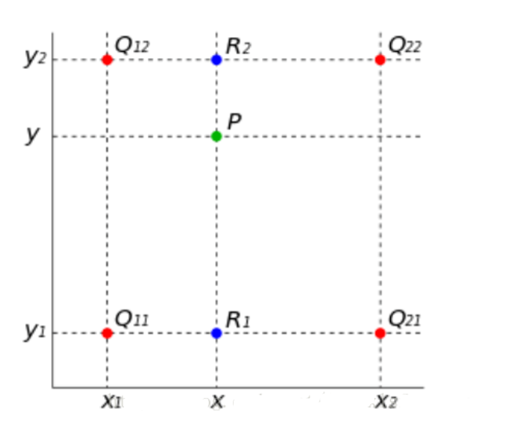
坐标:
srcX=dstX* (srcWidth/dstWidth) ,
srcY = dstY * (srcHeight/dstHeight)
坐标通过反向变换得到的浮点坐标为(i+u,j+v) (其中i、j均为浮点坐标的整数部分,u、v为浮点坐标的小数部分,是取值[0,1)区间的浮点数)
坐标对应值:f(i+u,j+v) = (1-u)(1-v)*f(i,j) + (1-u)v*f(i,j+1) + u(1-v)*f(i+1,j) + uv*f(i+1,j+1)
对比其他上采样方式,双线性插值的优势如下:
(1)最邻近元法计算量较小,但可能会造成插值生成的图像灰度上的不连续,在灰度变化的地方可能出现明显的锯齿状。
(2)双线性内插法性质,使高频分量受损,图像的计算比最邻近点法复杂,计算量较大,但没有灰度不连续的缺点,结果基本令人满意。它具有低通滤波轮廓可能会有一点模糊。
(3)三次曲线插值方法参数多,计算量比双线性插值要多得多,虽然效果好,但速度较慢。
(4)基于深度学习的上采样实际上就是通过训练转置卷积核对图片的尺寸进行扩充,当然为了取得好的效果,肯定不单单是一个转置卷积核就可以办到的,因此需要学习得到效果较好的卷积核,通用性可能没法保证。