队伍编号:CICC3280 团队名称:芯新星队
E203的乘法操作由一个17周期的乘法器实现。为了提升性能,该乘法器采用了基4Booth编码,将乘数分解为17个Booth编码,与被乘数相乘后形成的部分和再在相加,从而实现乘法运算。
考虑到E203的定位以及性能、功耗与芯片面积的平衡,E203采用了一些恰到好处的资源复用设计。
首先,乘法器每周器中的加法操作是通过复用ALU中的加法器实现的。由于乘法器本身是ALU的一个子模块,每一周期产生的部分积与之前累积的部分积可以通过ALU的数据通路部分传至ALU的加法器中相加。所以乘法器的设计本身并不需要额外的加法器。由于E203中所有需要计算加法的模块都采用了这种巧妙的设计,整E203中只使用了1个加法器便完成了所有操作。
其次,该乘法器实现了有效的寄存器复用。每一周期相加产生的部分积通过对乘数的位移操作而与乘数储存在同一组寄存器内,从而节省了一组寄存器的资源。
对于普通的乘法运算,以两个8比特二进制数为例,可以写为图一所示的8个部分积之和:
同理,两个32位二进制数相乘,在扩展符号位后,可以分为33个部分和之和。如果直接将33个部分和加起来,将耗费大量硬件资源,还有可能导致时序问题,拖慢处理器整体的频率。因此,使用Booth算法将部分和的数量减少。在使用Booth4算法时,可以将部分和减少为17个。
Booth算法的具体实现为:对于一个n比特的二进制数(设为A)来说,可以将其写为: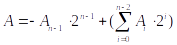
展开为: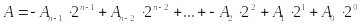
使用基4 Booth表示为: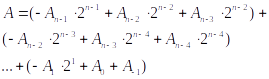
其中,
A_{-1}=0
所以,A×B可以表示为: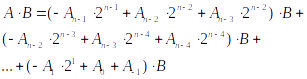
结合基4 Booth编码表如下:
| An+1 | An | An-1 | |
|---|---|---|---|
| 0 | 0 | 0 | +0 |
| 0 | 0 | 1 | +1 |
| 0 | 1 | 0 | +1 |
| 0 | 1 | 1 | +2 |
| 1 | 0 | 0 | -2 |
| 1 | 0 | 1 | -1 |
| 1 | 1 | 0 | -1 |
| 1 | 1 | 1 | 0 |
由此之前两个8比特数的乘法运算流程实现转化为图二所示:
以上就是e203内部乘法架构介绍,e203内部的乘法器采用的算法非常常见,巧妙的是其加法实现复用了e203alu内部的加法部件,极大程度地减少了硬件资源开销。