二进制除法器的本质是多次减法,直到余数小于除数为止。对应的两个N bit二进制数的除法算法如下。
1、设置2N bit寄存器A的低N位存放被除数,设置2N bit寄存器B的高N位存放除数,设置N bit寄存器C存放商,设置计数器cnt。
2、将A左移一位,与B比较高N位大小,若A[2N-1 : N] B[2N-1:N],则令A=A-B,令C左移一位,最低位为1;若A[2N-1:N] B[2N-1:N],则令C左移一位,最低为0;
3、计数器cnt加1,若小于N则继续进行步骤2,否则结束计算。
4、A中剩余的高N位为余数,C中的为商。
这种计算除法的算法被称为恢复余数除法,由于恢复余数除法采用串行结构,计算速度慢,且需要的时钟周期数不确定。
加减交替法是一种不恢复余数的除法。在恢复余数的除法中设第i次减法计算后的余数小于0,则恢复余数法的操作是,其中Y是除数,是余数。则第i+1次的余数如下式
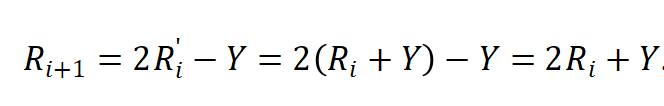
因此不恢复余数除法采用的公式,其结果与恢复余数后左移一位再减Y是等效的。
原码交替加减法的通用公式为: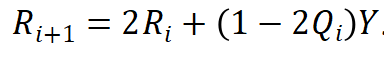
其中是第i次计算所得的商,则若部分余数为正,即,否则。
不恢复余数除法可以使用脉动阵列的形式,为此需引入可控加/减法单元(CAS)。
而如若要减小除法器的计算周期,可以通过并行处理的方式来提高除法器的计算性能