报名编号:CICC4035
团队名称:守序善良队
大家好,本篇是我们队伍的第一篇分享,主要内容是介绍牛顿-拉夫逊(Newton-Raphson)除法器原理。水平有限,如有错误,欢迎大家批评指正。
除法器是数字电路中的基础电路之一,也是CPU计算单元的核心功能之一。对于有符号整数除法操作,E203使用常用的加减交替法,然后使用迭代的方法,每个周期使用加法器生成部分余数,经过多个周期的迭代之后得到最终商和余数。其基本硬件原理图如图所示,从而实现多周期除法器。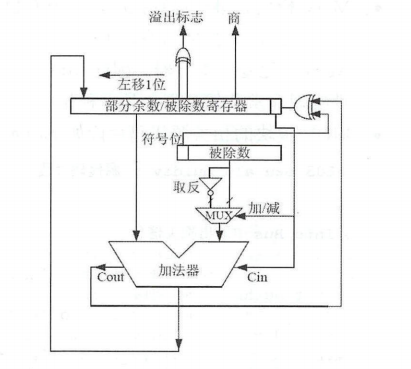
E203原有的除法器模块最终得到完全准确的除法结果,总共最多需要36周期,所需周期数较长,我们可以通过改进除法器算法缩短除法器周期,提高跑分性能。Newton-Raphson Method称牛顿-拉夫逊方法,又称牛顿迭代法。牛顿-拉夫逊方法是一种近似求解方程的根的方法。该方法使用函数f(x)的泰勒级数的前2项求解f(x)=0的根。将f(x)函数在点x0的某邻域内展开成n阶泰勒公式如下:
其中Rn(x)为n阶泰勒余项。令f(x)=0,取泰勒多项式的前2项作为近似,也就是1阶泰勒多项式;
则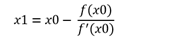
由此可得到迭代公式,依次迭代。
本文参考:
《手把手教你设计CPU》
https://zhuanlan.zhihu.com/p/400064205