团队编号:CICC1230
团队名称:少吃米饭多吃肉
对于cpu各类测试程序,设计一个高性能的硬件乘法器模块无疑是提分最快的法案,本文将从乘法算法开始,到rtl设计进行详细的解释说明,并附带一部分源码。
乘法器主要包括部分积的产生和部分积的压缩两部分,研究乘法器的方法一般是减少部分积的产生个数和提高部分积压缩的速度。
迭代乘法器与手算乘法最接近,对于一个n位宽的乘法运算,手算乘法是用n位乘数的每一位与n位被乘数的每一位相乘,总共相乘n次得到n个结果,这n个结果排列成阶梯形状,两两相加得到最终结果,迭代乘法器的原理也是如此。如下图迭代乘法器的结构所示: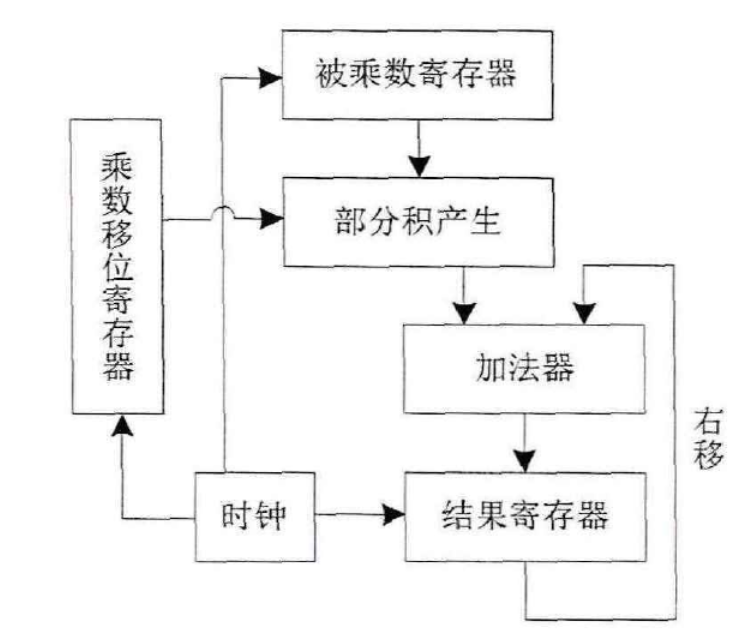
实现n位乘法运算的迭代乘法器需要n个加法器与2n个寄存器,乘数的最低位与被乘数相乘,结果保存到结果寄存器,该结果与下一次移位的乘数与被乘数的乘积相加。迭代乘法器的优点是使用的硬件资源较少且结构简单实现起来比较容易,但因为迭代一次需要等待一个时钟周所以迭代乘法器的效率很低延时很高,其延时随着位宽的增大而线性增大,对于n位乘法运算需要2n个时钟周期。
阵列乘法器基于迭代算法,是一种由进位保留加法器(CSA)为基本单元构成的乘法器结构,入下图所示是16位的线性阵列乘法器结构: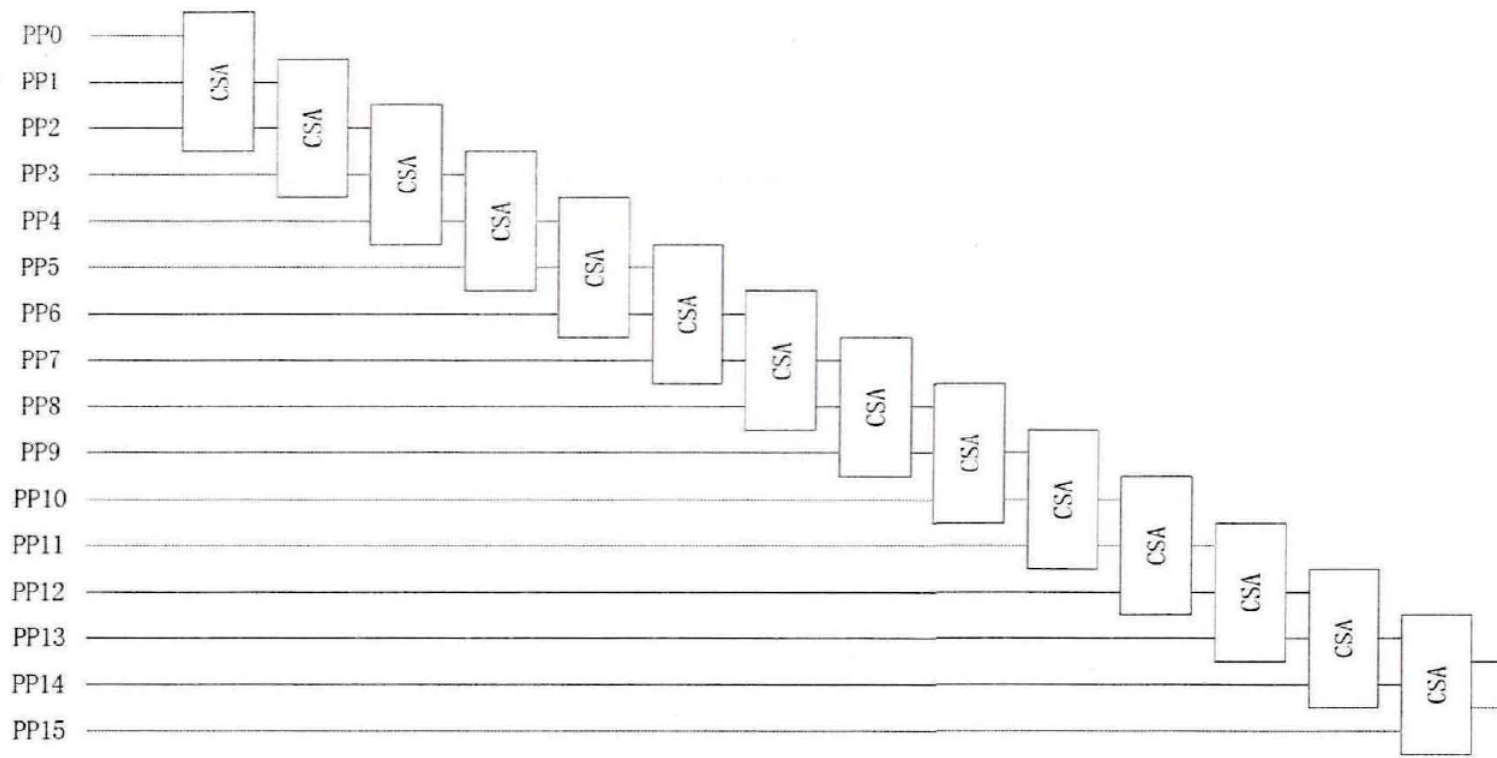
其中乘数的每一位都与被乘数相乘16位乘法产生16个部分积,三个低位的部分积相加通过CSA相加得到第一级的两个中间部分积,两个中间部分积与临近高位的一个部分积作为下个CSA的三个输入相加得到第二级两个部分积,按照这种操作一直进行,直到得到最终的两个部分积。
Booth乘法器采用Booth算法对乘数进行编码,一次编码的位数不同得到的部分积个数也不相同。大多数乘法器的优化都是采用此方法,下图是Booth乘法器的结构图: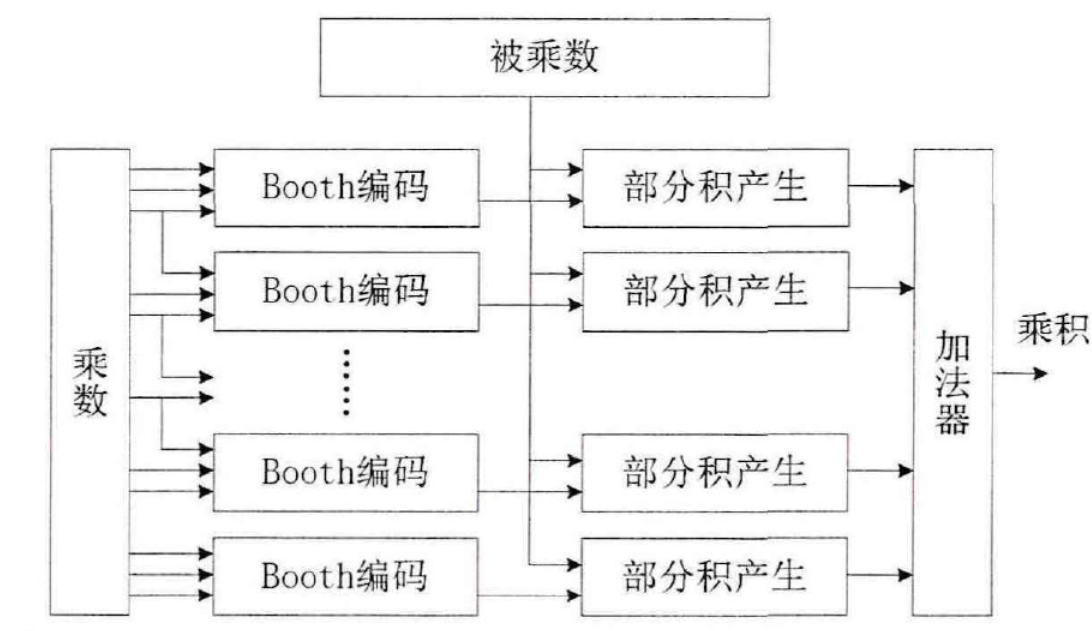
Booth乘法器减少了部分积个数从而提高乘法器的运算速度,但因为编码电路的存在导致硬件实现起来比迭代乘法器和阵列乘法器都要困难,且资源消耗比迭代乘法器和阵列乘法器要多
线性阵列乘法器结构简单实现起来较为容易,但每一级只有一个CSA起作用,所以有研究提出每一级有两个或者多个CSA并行地对部分积求和,其中较为经典的结构就是Wallace树形乘法器
下图给出了比较经典的华莱士树的结构: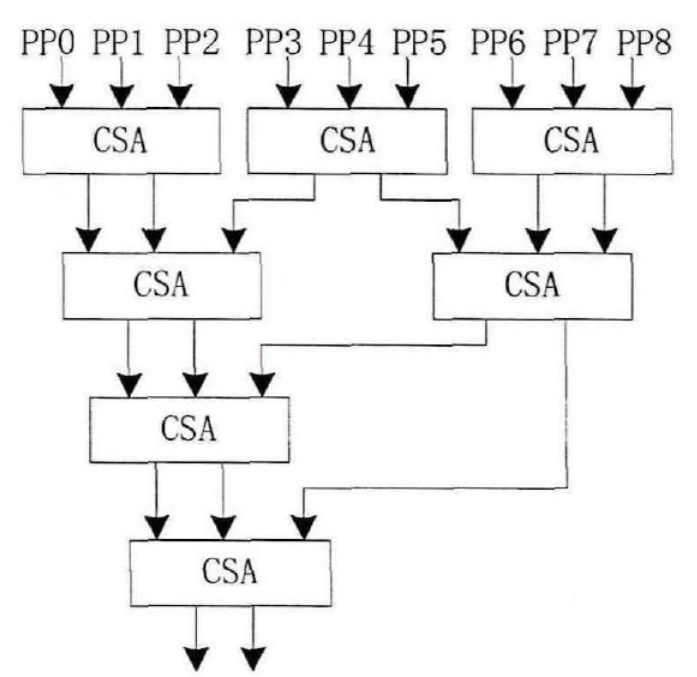
以一级CSA压缩为延时单位,对9个部分积进行压缩需要4级CSA压缩,共4个延时单位。而采用线性阵列乘法器压缩9个部分积需要7级CSA压缩,消耗7个延时单位,且Wallace树形乘法器消耗的CSA单元数量相对于线性阵列乘法器也大大减少。所以在对部分积进行压缩的时候,Wallace树形结构在延时以及资源消耗方面要明显优于线性阵列结构。Wallace树形结构的缺点是各级CSA之间的连线复杂,版图实现相对困难。
Booth乘法器通过减少产生的部分积个数提高乘法运算速度,Wallace树乘法器通过加快部分积压缩的速度提高乘法运算速度,将这两种乘法器结构的加速理念结合起来得到B-W混合乘法器结构,可以更有效的提高乘法器运算速度。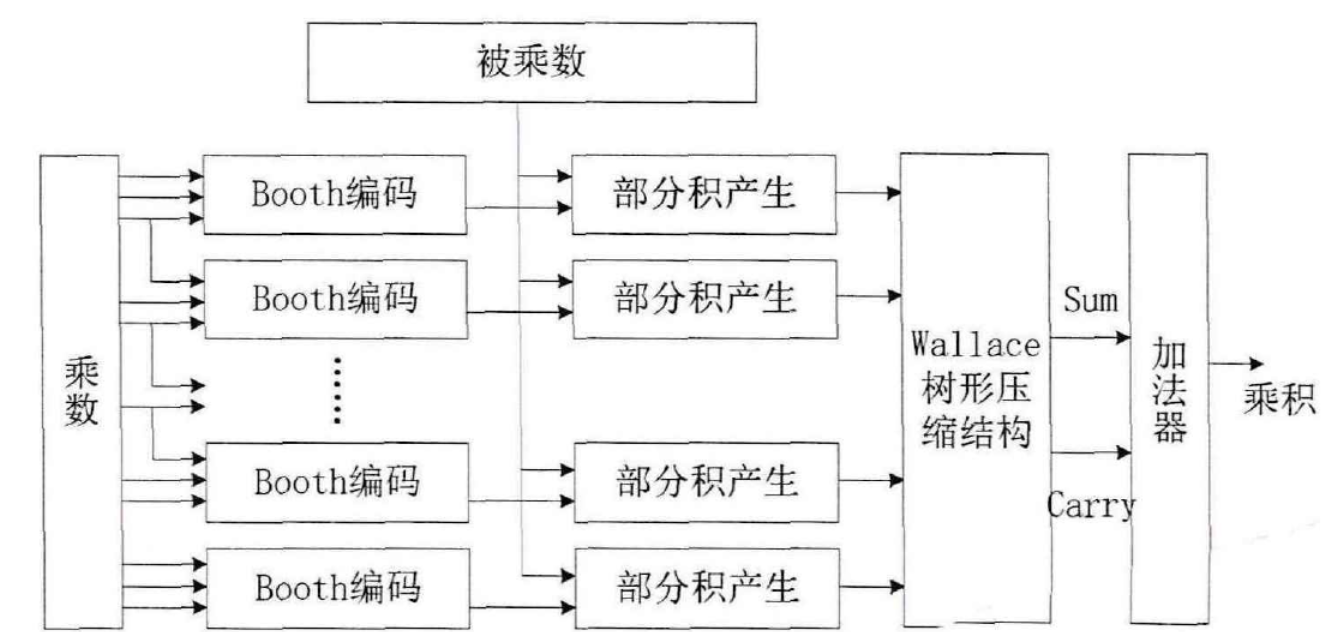
未完待续
结余:对于最后的Booth编码与不同的加法树组合可以得到各种PPA的乘法器结构,具体怎样实施就需要你明白设计的最重要的指标是什么