报名编号：CICC1740 团队名称：小型三极管
保留余数法：
保留余数法是一种数位迭代法，其实质是通过加减法实现除法运算。该算法从商的最高有效位开始，逐位进行试探性的减法，同时使用加法来保留余数。在循环中，加法和减法的操作方式取决于上一轮部分余数 Rj 的符号与被除数的符号是否一致。如果一致，则做减法，否则做加法，舍去符号位的进位。每轮操作得到的部分余数 R 左移一位，并进行减法。如果试探减法成功，则商位为“1”，继续进行循环操作直至结束。
Goldsmidit 算法:
这种类型的算法被公认为是目前性能最佳的算法，其核心思想可以用下面的公式表达：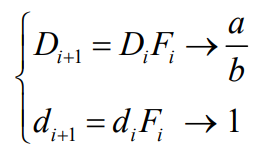

在这里，所使用的算法是函数迭代，其中被除数为D，除数为d，商为Q=D/d，分子为Di，分母为di，迭代因子为Fi[7]。通过数学方法，将除法运算转换为乘法运算，并迭代直到分子的值接近商值Q，分母接近1。然而，这种算法的缺点也非常明显，需要额外设计乘法器，这会影响乘法指令的周期，并且还需要对得到的结果进行额外的处理。
SRT 算法:
这种算法采用数值循环的基本思想，结构简单。其基本概念是，通过一次求商运算可以得到固定位数的商值，同时通过循环运算得到准商和余数值[8]。SRT算法通常采用查询基于Radix的查找表的方法来获得结果，常见的SRT算法有SRT4和SRT16。整个运算过程由加减法和移位操作完成，可以用以下方式描述：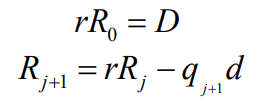

商选择函数为：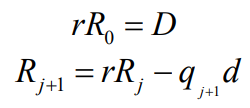

最终结果为：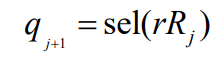

在这个算法中，Rj代表迭代循环j次后的部分余数值，d代表除数，D代表被除数，q代表商位。该算法的运算周期取决于不同基数的时钟计算，可以用公式n=log2 r来表示，其中n代表运算过程中产生的商位数，r为设定的基数[9]。例如，基数为2的算法在每次迭代中得到1位商位，基数为4的算法得到2位商位，基数为16的算法得到4位商位，基数为64的算法得到6位商位，以此完成多次循环迭代运算。