1.1 字与字节
用Z 表示 e-比特的向量集, Z 中的元素称为字, Z 中的元素称为字节。
1.2 S 盒
S 盒为固定的 8 比特输入 8 比特输出的置换,记为 Sbox(.)。
1.3 基本运算
在本算法中采用了以下基本运算:
⊕ 32 比特异或
<<< i 32 比特循环左移 i 位
1.4 密钥及密钥参量
加密密钥长度为 128 比特,表示为MK=(MK0, MK1, MK2, MK3),其中MKi(i=0,1,2,3)为 字。
轮密钥表示为(rk0, rk1, …, rk31),其中rki(i=0,…,31)为字。轮密钥由加密密钥生成。
FK=(FK0, FK1, FK2, FK3)为系统参数, CK=(CK0, CK1,…, CK31)为固定参数, 用于密钥扩 展算法,其中FKi(i=0,…,3) 、CKi(i=0,…,31)为字。
2 . 轮函数 F
本算法采用非线性迭代结构,以字为单位进行加密运算,称一次迭代运算为一轮变换。 设输入为(X 0 , X1 , X 2 , X 3 ) ∈ ( Z ) 4 ,轮密钥为 rk ∈ Z ,则轮函数 F 为:
F ( X0 , X1 , X2 , X3 , rk ) = X0 ⊕ T ( X1 ⊕ X2 ⊕ X3 ⊕ rk )
2.1 合成置换 T
T:Z → Z ,是一个可逆变换, 由非线性变换 τ 和线性变换 L 复合而成, 即 T(.)=L(τ(.))。
2.1.1 非线性变换τ
τ 由 4 个并行的 S 盒构成。
设输入为 A = (a0 , a1 , a2 , a3 ) ∈ (Z )4 , 输出为B = (b0 , b1 , b2 , b3 ) ∈ (Z )4 ,则 (b0 , b1 , b2 , b3 ) = τ(A) = ( Sbox (a0 ), Sbox (a1 ), Sbox (a2 ), Sbox (a3 ) )
2.1.2 线性变换 L
非线性变换 τ 的输出是线性变换 L 的输入。设输入为B ∈ Z ,输出为 C ∈ Z ,则 C = L(B) = B ⊕ (B <<< 2) ⊕ (B <<< 10) ⊕ (B <<< 18) ⊕ (B <<< 24)
2.2 S 盒
S 盒中数据均采用 16 进制表示。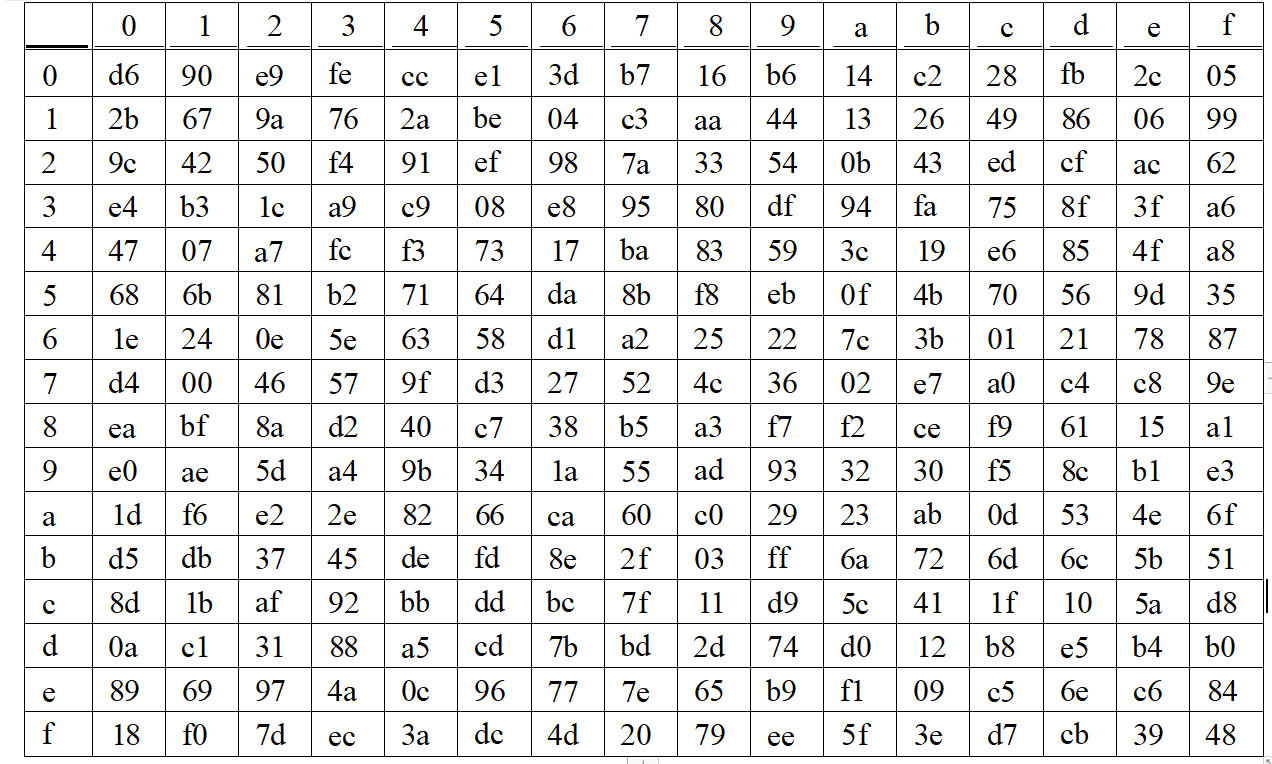
定义反序变换 R 为:
R ( A0 , A1 , A2 , A3 ) = ( A3 , A2 , A1 , A0 ) ,Ai ∈ Z , i = 0,1,2,3 。
设明文输入为 (X0 , X1 , X2 , X3 ) ∈ (Z)4 ,密文输出为(Y0 , Y1 , Y2 , Y3 ) ∈ (Z)4 ,轮密钥 为rki ∈ Z , i = 0,1,2,…,31 。则本算法的加密变换为:
Xi+4 = F(Xi , Xi+1 , Xi+2 , Xi+3 , rki ) = Xi ⊕ T(Xi+1 ⊕ Xi+2 ⊕ Xi+3 ⊕ rki ,) i = 0,1,…,31.
(Y0 , Y1 , Y2 , Y3 ) = R(X32 , X33 , X34 , X35 ) = (X35 , X34 , X33 , X32 )
。
本算法的解密变换与加密变换结构相同,不同的仅是轮密钥的使用顺序。
加密时轮密钥的使用顺序为: (rk0, rk1, …, rk31 )
解密时轮密钥的使用顺序为: (rk31, rk30, …, rk0 )
本算法中加密算法的轮密钥由加密密钥通过密钥扩展算法生成。
加密密钥MK=(MK0, MK1, MK2, MK3) ,MKi ∈ Z ,i =0,1,2,3;
令Ki ∈ Z ,i =0,1,…,35,轮密钥为 rk i ∈ Z , i = 0 ,1,…, 31 ,则轮密钥生成方法为: 首先, (K0,K1,K2,K3)=(MK0 ⊕FK0,MK1⊕FK1,MK2⊕FK2,MK3⊕FK3)
然后, 对i = 0 ,1, 2 ,…, 31 :
rki = Ki +4 = Ki ⊕ T′(Ki +1 ⊕ Ki +2 ⊕ Ki +3 ⊕ CK i )