损失函数(loss function)是用来衡量预测值和真实值差距的函数,是模型优化的目标,所以也称之目标函数、优化评分函数。这是机器学习中很重要的性能衡量指标, 评价函数和损失函数相似,只是关注点不同:损失函数用于训练过程,而评价函数用于模型训练完成后(或每一批次训练完成后)的度量,所以这里放到一个篇幅里介绍。
keras提供的损失函数如下,它们有自己适用的应用场景,最常用的是均方误差和交叉熵误差:
| 编号 | 可用损失函数 | alias | 说明 |
|---|---|---|---|
| 1 | mean_squared_error(y_true, y_pred) | mse | MSE 均方误差 |
| 2 | mean_absolute_error(y_true, y_pred) | mae | MAE 平均绝对值误差 |
| 3 | mean_absolute_percentage_error(y_true, y_pred) | mape | MAPE 平均绝对百分比误 |
| 4 | mean_squared_logarithmic_error(y_true, y_pred) | msle | MSLE 对数方差 |
| 5 | hinge(y_true, y_pred) | 合页 | |
| 6 | squared_hinge(y_true, y_pred) | 平方合页 | |
| 7 | categorical_hinge(y_true, y_pred) | 多类合页 | |
| 8 | log_cosh(y_true, y_pred) | logcosh | 双曲余弦对数误差 |
| 9 | categorical_crossentropy(y_true, y_pred) | 分类交叉熵 | |
| 10 | sparse_categorical_crossentropy(y_true, y_pred) | 稀疏交叉熵 | |
| 11 | binary_crossentropy(y_true, y_pred) | bce | BCE二进制交叉熵 |
| 12 | kullback_leibler_divergence(y_true, y_pred) | kld | KL散度 |
| 13 | poisson(y_true, y_pred) | 泊松损失 | |
| 14 | cosine_proximity(y_true, y_pred) | 余弦相似度 |
以下是各个误差函数的详细介绍:
1 mean_squared_error(MSE)
mean_squared_error即均方误差,一般用于回归计算,是最常用的损失函数,但在某些情况下,其它损失函数可能更适合。
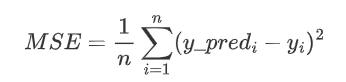
losses中的源码为:
def mean_squared_error(y_true, y_pred):
return K.mean(K.square(y_pred - y_true), axis=-1)2 mean_absolute_error(MAE)
mean_absolute_error即平均绝对误差,一般用于回归计算,与MSE一样都是测量两个向量(预测向量与目标值)之间距离的方法,只不过MSE使用的是平方和的平均值,而MAE使用绝对值的平均值。
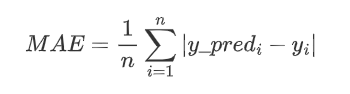
其源码为:
def mean_absolute_error(y_true, y_pred):
return K.mean(K.abs(y_pred - y_true), axis=-1)选择MSE还是MAE?
MSE是误差的平方和,所以对于异常数据更为敏感。如果异常值表示的反常现象对于业务非常重要,且应当被检测到,那么我们就应当使用MSE。另一方面,如果我们认为异常值仅表示损坏数据而已,那么我们应当选择MAE作为损失函数。
3 mean_absolute_percentage_error (MAPE)
平均绝对值百分比误差,它是一种相对度量,以百分比为单位而不是变量的单位,一般用于回归计算,一般用于各种时间序列模型的预测,如销量预测等。
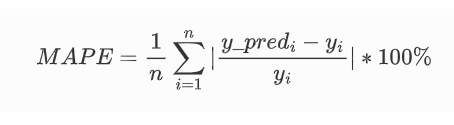
其源码为:
def mean_absolute_percentage_error(y_true, y_pred):
diff = K.abs((y_true - y_pred) / K.clip(K.abs(y_true), K.epsilon(), np.inf))
return 100. * K.mean(diff, axis=-1)4 mean_squared_logarithmic_error(MSLE)
对数方差,适用于目标具有指数增长趋势,例如:人口数量,跨年度商品的平均销售额等。
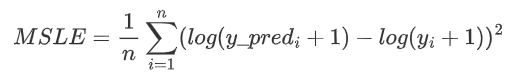
其源码为:
def mean_squared_logarithmic_error(y_true, y_pred):
first_log = K.log(K.clip(y_pred, K.epsilon(), np.inf) + 1.)
second_log = K.log(K.clip(y_true, K.epsilon(), np.inf) + 1.)
return K.mean(K.square(first_log - second_log), axis=-1)5 hinge (Hinge)
合页,通常用于“maximum-margin”二分类任务中,如SVM支持向量机
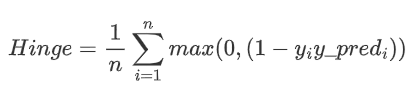
其源码为:
def hinge(y_true, y_pred):
return K.mean(K.maximum(1. - y_true * y_pred, 0.), axis=-1)6 squared_hinge (SH)
平方合页,与hinge类似,最大值时加上平方值,与常规hinge合页损失相比,平方合页损失函数对离群值惩罚更严厉,一般多用于二分类计算。
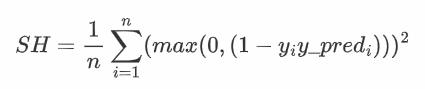
其源码为:
def squared_hinge(y_true, y_pred):
return K.mean(K.square(K.maximum(1. - y_true * y_pred, 0.)), axis=-1)7 categorical_hinge
多类合页,更多用于多分类形式。
其源码为:
def categorical_crossentropy(y_true, y_pred):
'''Expects a binary class matrix instead of a vector of scalar classes.
'''
return K.categorical_crossentropy(y_pred, y_true)8 logcosh
双曲余弦对数误差函数,它比MSE损失更平滑。对于较小的 x , logcosh近似等于 (x ** 2) / 2 。对于大的 x,近似于 abs(x) - log2 。这表示 'logcosh' 与均方误差算法大致相同,但是不会受到偶发性错误预测的强烈影响。
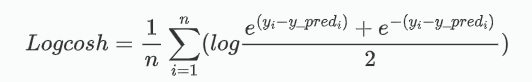
其源码为:
def logcosh(true, pred):
loss = np.log(np.cosh(pred - true))return np.sum(loss)9 categorical_crossentropy(CCE)
分类交叉熵,主要用于分类算法,当使用categorical_crossentropy损失函数时,目标值格式应该为one-hot编码格式。可以使用keras的to_categorical(int_labels, num_classes=None)将整数目标值转为one-hot编码

其源码为:
def categorical_crossentropy(y_true, y_pred):
'''Expects a binary class matrix instead of a vector of scalar classes.
'''
return K.categorical_crossentropy(y_pred, y_true)10 sparse_categorical_crossentropy(SCCE)
稀疏交叉熵,与CCE分类交叉熵相类似,主要用于分类算法,只是目标格式输出值略有不同,CCE以one-hot编码输出,而SCEE直接转化为索引值进行输出。
其源码为:
def sparse_categorical_crossentropy(y_true, y_pred):
'''expects an array of integer classes.
Note: labels shape must have the same number of dimensions as output shape.
If you get a shape error, add a length-1 dimension to labels.
'''
return K.sparse_categorical_crossentropy(y_pred, y_true)11 binary_crossentropy(BCE)
二进制交叉熵,更适用于二分类,对于二分类问题,BCE的运行效率会更高,注意:如果使用BCE作为损失函数,则节点介于[0, 1]之间,意味着在最终输出需要使用sigmoid激活函数。
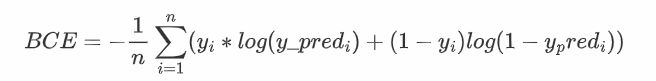
其源码为:
def binary_crossentropy(y_true, y_pred):
return K.mean(K.binary_crossentropy(y_pred, y_true), axis=-1)12 kullback_leibler_divergence
KL散度,用于分类计算,通过衡量预测值概率分布到真值概率分布的相似度差异,在运动捕捉里面可以衡量未添加标签的运动与已添加标签的运动,进而进行运动的分类。
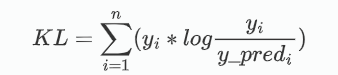
其源码为:
def kullback_leibler_divergence(y_true, y_pred):
y_true = K.clip(y_true, K.epsilon(), 1)
y_pred = K.clip(y_pred, K.epsilon(), 1)
return K.sum(y_true * K.log(y_true / y_pred), axis=-1)13 poisson
泊松损失函数,用于回归算法,一般用于计算事件发生的概率。
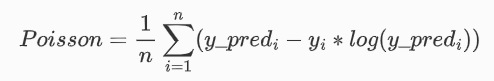
其源码为:
def poisson(y_true, y_pred):
return K.mean(y_pred - y_true * K.log(y_pred + K.epsilon()), axis=-1)14 cosine_proximity
余弦相似度,预测值与真实标签的余弦距离平均值的相反数,它是一个介于-1和1之间的数字。当它是负数时在-1和0之间,0表示正交,越接近-1 表示相似性越大,值越接近1表示不同性越大,这使得它在设置中可用作损失函数。如果' y_true '或' y_pred '是一个零向量,余弦无论预测的接近程度如何,则相似度都为 0,而与预测值和目标值之间的接近程度无关。
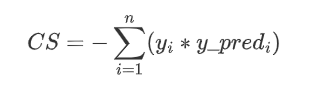
其源码为:
def cosine_proximity(y_true, y_pred):
y_true = K.l2_normalize(y_true, axis=-1)
y_pred = K.l2_normalize(y_pred, axis=-1)
return -K.mean(y_true * y_pred, axis=-1)一般情况下,并不需要我们自定义损失函数,keras提供的损失函数基本够用,某些特殊情况,我们可以自己定义损失函数。
def my_loss(y_true,y_pred):
return K.mean((y_pred - y_true),axis = -1)
model.compile(loss=my_loss, optimizer='SGD', metrics=['accuracy'])注意:keras 损失函数以(y_true, y_pred)作为入参。
from keras import losses
# 写法1:
model.compile(loss='mean_squared_error', optimizer='sgd')
# 写法2:
model.compile(loss=losses.mean_squared_error, optimizer='sgd')
# 写法3:如果有别名,也可以使用别名
model.compile(loss='mse', optimizer='sgd')回归问题使用mean_squared_error(均方误差)
二分类问题使用 binary_crossentropy
多分类问题使用 categorical_crossentropy (最后一层使用softmax激活函数),非one-hot编码使用 sparse_categorical_crossentropy
下面比较一下categorical_crossentropy(分类交叉熵)与 sparse_categorical_crossentropy(稀疏交叉熵)
使用sparse_categorical_crossentropy:
import tensorflow as tf
import tensorflow.keras as keras
import numpy as np
print(keras.__version__)
(x_train, y_train), (x_valid, y_valid) = keras.datasets.mnist.load_data()
assert x_train.shape == (60000, 28, 28)
assert x_valid.shape == (10000, 28, 28)
assert y_train.shape == (60000,)
assert y_valid.shape == (10000,)
print("y_valid type is %s" % (y_valid.shape))
# step1: use sequential
model = keras.models.Sequential()
# step2: add layer
model.add(keras.layers.Flatten(input_shape=(x_train.shape[1], x_train.shape[2])))
model.add(keras.layers.Dense(units=784, activation="relu", input_dim=784))
model.add(keras.layers.Dense(units=10, activation="softmax"))
# step3: compile model
model.compile(optimizer="Adam", loss='sparse_categorical_crossentropy', metrics=['accuracy'])
print("model:")
model.summary()
# step4: train
model.fit(x_train, y_train, batch_size=64, epochs=5)
# step5: evaluate model
model.evaluate(x_valid, y_valid)
# save model
#model.save('keras_mnist.h5')
img = x_valid[0]
img = np.reshape(img, (-1, 28, 28))
output = model.predict(img)
print("output type is %s" % (type(output)))
print(output)
predict_num = np.argmax(output, axis = 1) # 需要使用np.argmax找到最大值
print("predict num is %d" % predict_num)使用categorical_crossentropy:
将上述代码的loss直接换为categorical_crossentropy,运行时会报错
ValueError: Shapes (None, 1) and (None, 10) are incompatible需要将label转换为one-hot编码,代码如下:
import tensorflow as tf
import tensorflow.keras as keras
import numpy as np
print(keras.__version__)
(x_train, y_train), (x_valid, y_valid) = keras.datasets.mnist.load_data()
assert x_train.shape == (60000, 28, 28)
assert x_valid.shape == (10000, 28, 28)
assert y_train.shape == (60000,)
assert y_valid.shape == (10000,)
y_train_cate = keras.utils.to_categorical(y_train, 10) # 将y_train转为one-hot编码
y_valid_cate = keras.utils.to_categorical(y_valid, 10) # 将y_valid转为one-hot编码
print("y_valid shape is %d" % (y_valid.shape))
# step1: use sequential
model = keras.models.Sequential()
# step2: add layer
model.add(keras.layers.Flatten(input_shape=(x_train.shape[1], x_train.shape[2])))
model.add(keras.layers.Dense(units=784, activation="relu", input_dim=784))
model.add(keras.layers.Dense(units=10, activation="softmax"))
# step3: compile model
model.compile(optimizer="Adam", loss='categorical_crossentropy', metrics=['accuracy']) # loss使用categorical_crossentropy
print("model:")
model.summary()
# step4: train
model.fit(x_train, y_train_cate, batch_size=64, epochs=5)
# step5: evaluate model
model.evaluate(x_valid, y_valid_cate) # 评估时使用categorical_crossentropy
# save model
#model.save('keras_mnist.h5')
img = x_valid[0]
img = np.reshape(img, (-1, 28, 28))
output = model.predict(img)
print(output.shape)
print(output)
predict_num = np.argmax(output, axis = 1)
print("predict num is %d" % predict_num)目前只是比较了使用方法的不同,后续有时间分析一下不同loss函数的内在差异。
评价函数和损失函数相似,不同的是损失函数用于训练过程(参与反向传播),而评价函数仅用于模型的度量,记录在每个epoch的末尾。
在应用方面,keras.losses中定义的所有函数均可作为评价函数使用,此外,keras.metrics额外定义了6个评价函数。
| 编号 | 可用的评价函数 | alias | 说明 |
|---|---|---|---|
| 1 | accuracy(y_true, y_pred) | acc | 对比结果 |
| 2 | binary_accuracy(y_true, y_pred, threshold=0.5) | 可用于二元分类的评价(大于threshold设为1,否则设为0) | |
| 3 | categorical_accuracy(y_true, y_pred) | 可用于多元分类one-hot标签的评价(one-hot标签) | |
| sparse_categorical_accuracy(y_true, y_pred) | 可用于多元分类的评价(非one-hot标签) | ||
| 5 | top_k_categorical_accuracy(y_true, y_pred, k=5) | 可用于前k项分类的评价,前k值中存在目标类别即认为预测准确(one-hot标签) | |
| 6 | sparse_top_k_categorical_accuracy(y_true, y_pred, k=5) | 可用于前k项分类的评价(非one-hot标签) |
# 可以测量多个指标 metrics 入参为列表
model.compile(loss='mse', optimizer='SGD', metrics=['accuracy', 'mse'])这样就可以同时评估accuracy以及mse了, 记录在每个epoch的末尾。
参考: