MD5算法的输入字符串消息转换为二进制长度范围应在0比特 到(2^64-1)比特之间,因为二进制输入串的最后64比特是用来存储输入长度。而在MD5算法输入中,如果二进制输入字符串的位长度超出了(2^64-1)比特,则把 (二进制输入长度%2^64)存储在最后一组数据的最后64比特中。然后经过预处理后,输入二进制字符串就会成为512-bit为一组的消息,并将每一组512-bit的消息分成16个32位的消息块,表示为:message_var[0]、message_var[1]……message_var[15]。经过MD5算法64轮处理后,输出一个位长为128-bit消息摘要,它是由最初4个32-bit就储存器级联组成的。
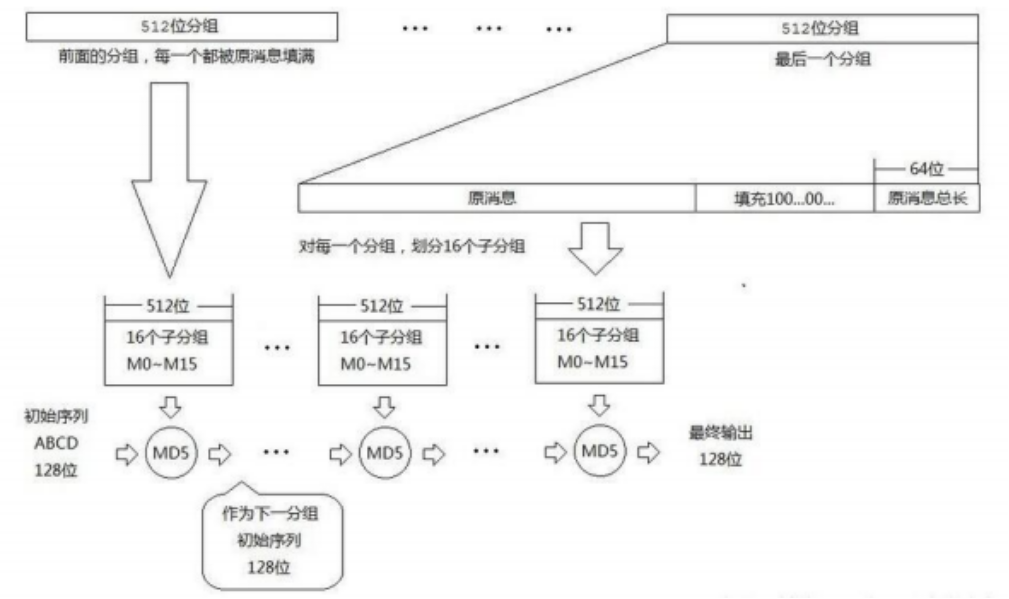
图1 MD5 算法的整体流程图
Fig. 1 Overall flow chart of MD5 algorithm
MD5消息填充规则:
①填充后的数据位数必须是512*N(N为整数);
②在填充数据最后一个数据中最后64位存放消息长度;
③MD5是“小端模式”。
填充后的二进制数据位宽一定是512的整数倍,是因为在MD5的哈希运算中,每次的输入是以512-bit为单位,然后进入运算。需要注意的是,消息的长度是指将输入的数据通过ASCII码转换为二进制后所占的位数,而非字符串本身长度。
【举例1】:输入信息为“qust”,转换为二进制为“0111_0001 0111_0101 0111_0011 0111_0100”。这里通过ASCII表查找出相对应的ASCII码,把输入字符串信息“qust”转换为二进制数据。每一个ASCII码占8-bit,所以一共占有4*8=32位。消息长度为32,转换为二进制为“0010_0000”。这里需要留心的是消息长度不是4,不是取字符串的长度,而是二进制数据长度。
MD5算法填充规则如下:
①先把输入的字符串数据转换为二进制数据;
②而后通过运用多个“0”和一个“1”进行填充,“1”为结束标志位,需要加在消息的结束位置,然后填充多个“0”知道数据第448位,最后再加上64-bit的消息长度,总长度共512-bit。
【举例2】:假如输入字符串为“qust”:
首先,我们需要将“qust”转换成二进制字符串如下所示:
0111_0001 0111_0101 0111_0011 0111_0100
补位操作如图1.2所示:

图 1.2 MD5 补位操作
Fig. 1.2 Filling operation
“1”作为结束标志位是必须要有,但有一种特殊情况,就是当输入消息长度为448-bit,这时恰好剩余64-bit空间,这恰好可以容纳“消息长度”。但这种做法却没有结束标志位“1”,故不可取。而应该在448-bit消息后加上结束标志位“1”。而后在结束标志位后面填充511个0,最后再加上64-bit的二进制消息长度。这时,本来最后一组数据就被填充为512-bit*2。
定义一个16*32位寄存器数组message_var。假设i为0~15的一个整数,message_var[i]就代表第i个message_var的32-bit寄存器,这就相当于初始化了16个32-bit寄存器。而在消息填充(padding)中我们已经得到512*N数据,然后再消息生成(Message Schedule)中吧512-bit数据分别保存在这16个寄存器当中。
【举例3】:
将消息填充(padding)中结果命名为“Q”,则message_var[i]=Q[(32*i):(32*i+31)]。
此部分为MD5算法的核心。MD5有4组主循环,每组的主循环需要进行16轮哈希运算,总计64轮哈希运算,而且每组所对应的非线性变化是不同的。然后会对32-bit message_var[i]进行计 算,最终得到一个位宽为128-bit的消息摘要(Message Diges)。每轮哈希运算需要一种32-bit输出与三种不同的32-bit输入。输入包括4个32bit的哈希值(Hash Value):a,b,c,d;常量:T[i];message_var[i]值。输出包括4个32-bit的哈希值a,b,c,d。
步骤如下:
首先对链接变量a,b,c,d赋初值;因为第一轮哈希运算无上一轮的哈希值可以作为输入,故需要4个初始化变量作为输入,如表1-1。
表1-1链接变量
Table 1-1 Link variable
寄存器 | 大端输入 | 小端输入 |
A | 0x01234567 | 0x67452301 |
B | 0x89abcdef | 0xEFCDAB89 |
C | 0xfedcba98 | 0x98BADCFE |
D | 0x76543210 | 0x10325476 |
定义四个非线性函数,如表1-2:
表1-2非线性函数
Table 1-2 Non-linear function
轮数 | 布尔函数 | Func(b,c,d) |
1 | F(b,c,d) | (b&c)|((~b)&d) |
2 | G(b,c,d) | (b&d)|(c&(~d)) |
3 | H(b,c,d) | b+c+d |
4 | I(b,c,d) | c+(b|(~d)) |
message_var[i]表示消息中的一组数据的第i个子分组(从0到15),常数ti=2^32*abs(sin(j))的取整部,j:1~64,单位是弧度。
FF(a, b, c, d, message_var[i], s, ti)表示a = b + ((a + F(b,c,d) + Mj + ti) <<
GG(a, b, c, d, message_var[i], s, ti)表示a = b + ((a + G(b,c,d) + Mj + ti) <<
HH(a, b, c, d, message_var[i], s, ti)表示a = b + ((a + H(b,c,d) + Mj + ti) <<
II(a, b, c, d, message_var[i], s, ti)表示a = b + ((a + I(b,c,d) + Mj + ti) <<
其中:明文字Mj的顺序如表1-3所示:
表1-3明文字Mj的顺序
Table 1-3 The order of plain text Mj
步骤 | 名文字的顺序 |
1,2,……,15 | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
16,17,……,31 | 1 6 11 0 5 10 15 4 9 14 3 8 13 2 7 12 |
32,33,……,47 | 5 8 11 14 1 4 7 10 13 0 3 6 9 12 15 2 |
48,49,……,63 | 0 7 14 5 12 3 10 1 8 15 6 13 4 11 2 9 |
每次操作中循环左移S的比特数如表所示:
MD5算法中64步运算循环左移数s
表1-4 循环左移数s
Table 1-4 Cycle left shift s
步骤 | 名文字的顺序 |
1,2,……,15 | 7 12 17 22 7 12 17 22 7 12 17 22 7 12 17 22 |
16,17,……,31 | 5 9 14 10 5 9 14 10 5 9 14 10 5 9 14 10 |
32,33,……,47 | 4 11 16 23 4 11 16 23 4 11 16 23 4 11 16 23 |
48,49,……,63 | 6 10 15 21 6 10 15 21 6 10 15 21 6 10 15 21 |
MD5信息摘要算法中的运算设计流程如图1.3所示。
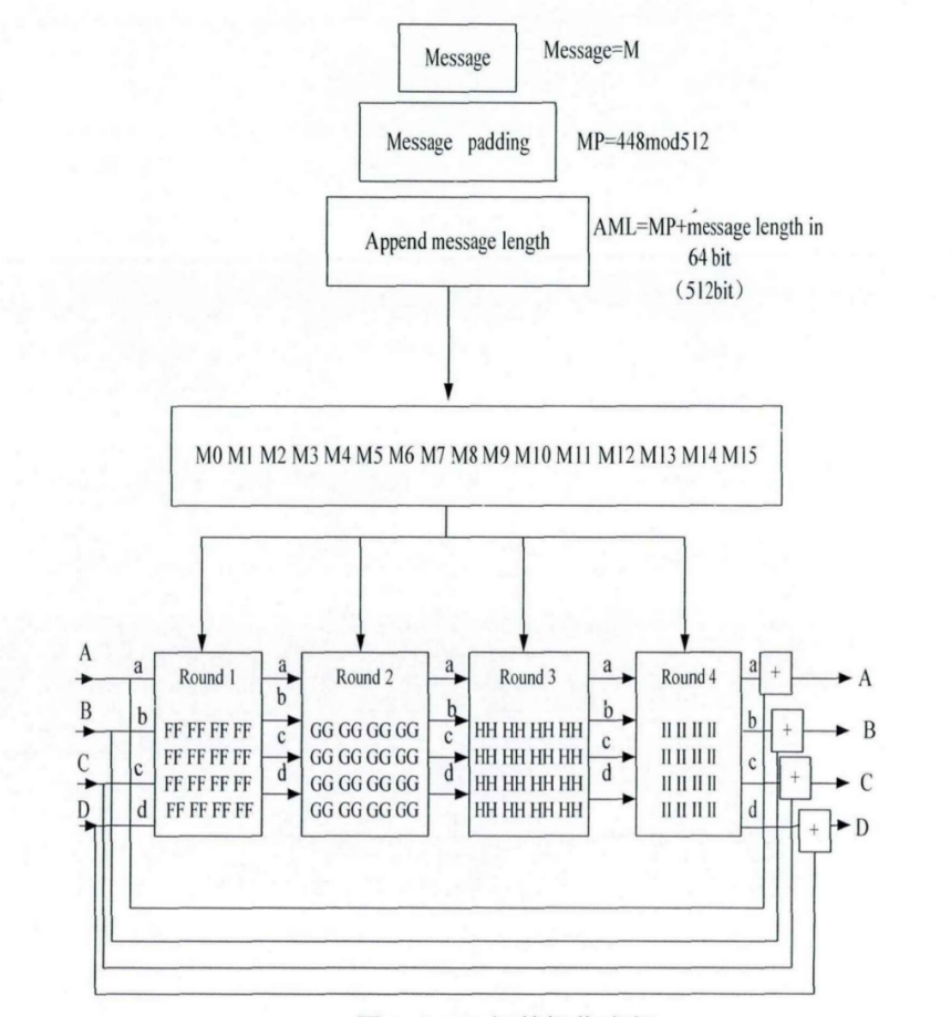
图1.3 MD5 算法运算流程
Fig. 1.3 MD5 Algorithm operation flow
每一轮MD5信息摘要运算操作流程如图1.4所示:
图1.4MD5 算法运算操作
Fig. 1.4 MD5 algorithm operation
4轮64歩操作实现之后,将32位宽比特的链接变量A、 B、 C、 D分别加上已经完成迭代后32位宽比特的a、 b、 c、 d。
A=A + a B=B + b C=C + c D=D + d
而且继续参与下一个512位分组数据中链接变量的初始值,重复2、3步骤,直到完成所有的分组,最后的输出是32位的A、 B、 C和D的级联成128位的信息摘要。
然后将其转换为大端输出。
【注:MD5算法的计算都是按照小端模式。】
【举例3】
“qust”消息摘要为:“fc476bfe_d50a6744_61c9c029_2d92d7ab