队伍编号:CICC3280 团队名称:芯新星队

e203内部除法操作使用加减交替迭代法进行运算，除几个特殊运算外，正常的除法操作需要33个周期才能输出运算结果，极大程度地影响了系统的性能。我们对e203的除法器进行了新的算法实现并改进。目前高性能的除法运算大多使用SRT-4算法进行设计。下面对其硬件算法进行讲解。

SRT-4算法原理公式推导：根据除法的数学定义而言：

x=qD+rem

（其中表示x表示被除数，D表示除数，q表示商，rem表示余数）
利用数学递归算法进行将除法操作简化为迭代算法，每次迭代产生一个基数为$\beta$的商。经过$j$次迭代后，产生的商值表示为：
q{j}=\sum{i=0}^j q_i \beta^{j-i}
假设需要迭代次才能得到最终的商值，因此最终的商值表示为：
q=q_n=\sum{i=0}^n qi \beta^{n-i}
为方便计算，采取先将被除数与除数进行预处理即将上述等式同时除以$\beta^{n}$。得到简便的商值确定表达式：
q=q_n=\sum{i=0}^n qi \beta^{-i}
因此最终正确的除法表达式可简化为：
rem=\beta^n(x-dq{n})
将表达式进行迭代展开，即每一次选商的迭代进行可以表示为：

r{i}=\beta r{i-1}-q{i}D

（其中r{i}表示第i次部分余数，r{i-1}表示第i-1次的部分余数，\beta表示选择的基数在SRT-4算法中为4，q{i}表示i次的选商结果）

传统的SRT-4算法选商的基本原理便是利用PD图实现选商的过程。（针对SRT-4算法的冗余数字集设置为最小冗余度{-2，-1，0，1，2}，冗余度因子$\rho=2/3$)。

PD图实现选商：利用PD图可以直观地看到每个商值的交集，通过划分交集的归属区域便可实现对传统SRT-4算法选商表的构建。

在对商值区域进行划分时，主要应用不等式条件：

(-\frac{2}{3}+q)D\le P\le (\frac{2}{3}+q)D

（其中表示P该次的部分余数，q表示该次的商值），借助不等式(7)可以确定传统SRT-4算法的PD图（如图八所示）。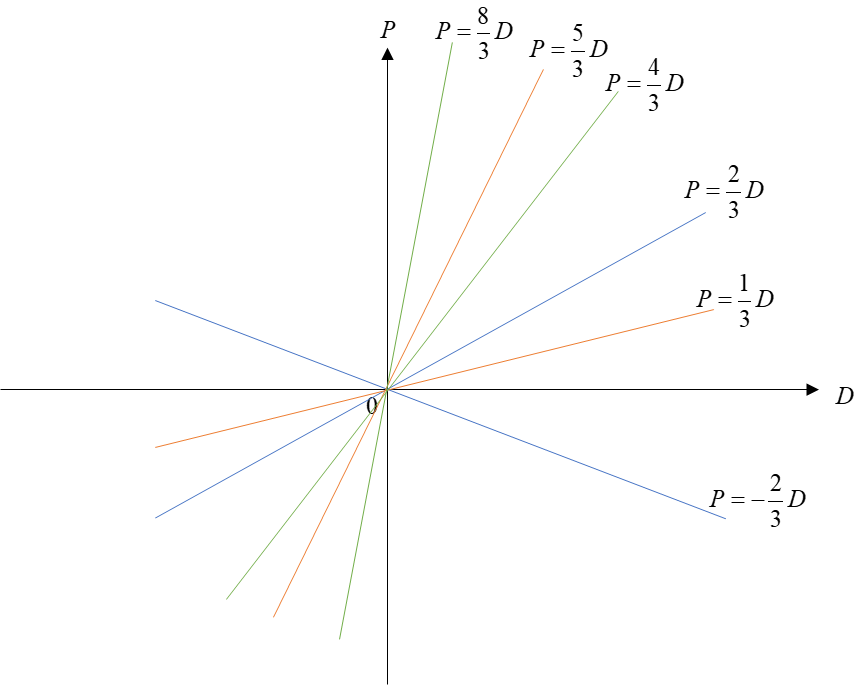

可以看出，构建传统SRT-4算法选商表需要确定多个选商值（即需要划分除数的区间，并且需要将被除数与除数区间内的选商值进行比较）。

由于论坛部分Markdown格式问题，对于MathJex语法的支持不尽完善，具体的公式实现需要具体了解的，可以自行百度相关算法以及查阅相关论文进行学习。

本队对于除法部件的实现借助于快速选商表采用了创新的双快速SRT-4算法，有兴趣的同学可以自行思考并设计。